Idris入門: 二分木
κeenです。Idris入門: 数当てゲーム | κeenのHappy Hacκing Blogに続いて入門記事を書いてみます。 前回はバイナリを作ったので今回はライブラリを作ります。題材は(非平衡)二分木。
非平衡なのは平衡にすると複雑になるのと、平衡にするときは別のネタ(依存型)があるのでそれまでとっておくためです。
対象読者は前回の数当てゲームのチュートリアルを終えた人に設定します。
今回のコード全体像はこちらにあります。
プロジェクト作成
以下のような構成でディレクトリを作りましょう。
├── btree.ipkg
└── src
└── BTree.idr
btree.ipkgには以下を書きます。
package btree
sourcedir = src
modules = BTree
そして BTree.idr に今から二分木を実装していきます。
二分木とは
二分木はデータ構造です。 値の保持、検索、削除ができるので集合やKey-Valueストアの実装に使われます。 手続き型言語ではそれらの実装にハッシュセットやハッシュマップがよく使われますが、関数型言語では二分木の方がよく使われるようです。
二分木はノード(節)とリーフ(葉)からなります。リーフは何もデータを持ちません。 ノードは1つの値と2つ(左右)の子(部分木)を持ちます。 ノードには「ノードの左の子に保持されている全ての値よりもノードの保持している値の方が大きい。ノードの右の子に保持されている全ての値よりも値の方が小さい。」という条件が成つように作ります。
図にするとこんな感じでしょうか
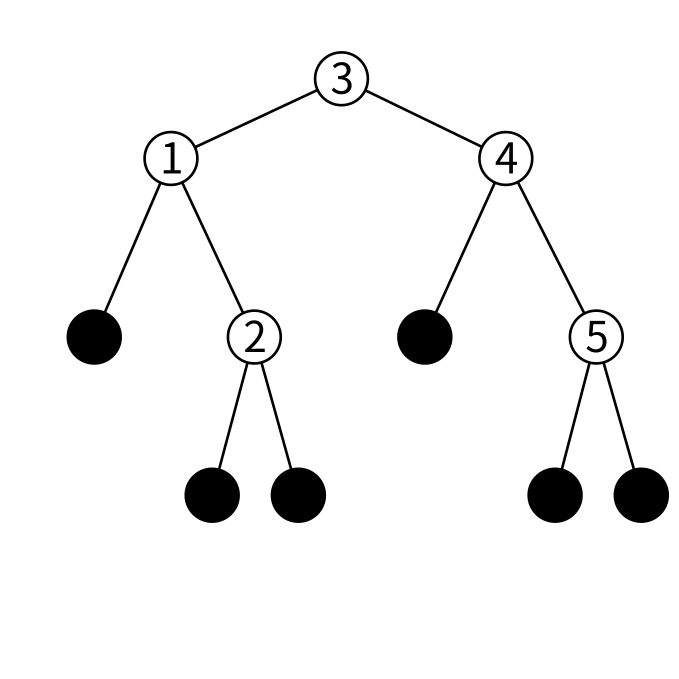
1, 2, 3, 4, 5がノードに保持されている値です。一番上にあるノード(ここでは3を保持しているノード)を根と呼びます。 「ノードの左の子に保持されている全ての値よりもノードの保持している値の方が大きい。ノードの右の子に保持されている全ての値よりも値の方が小さい。」という条件もちゃんと成り立っています。
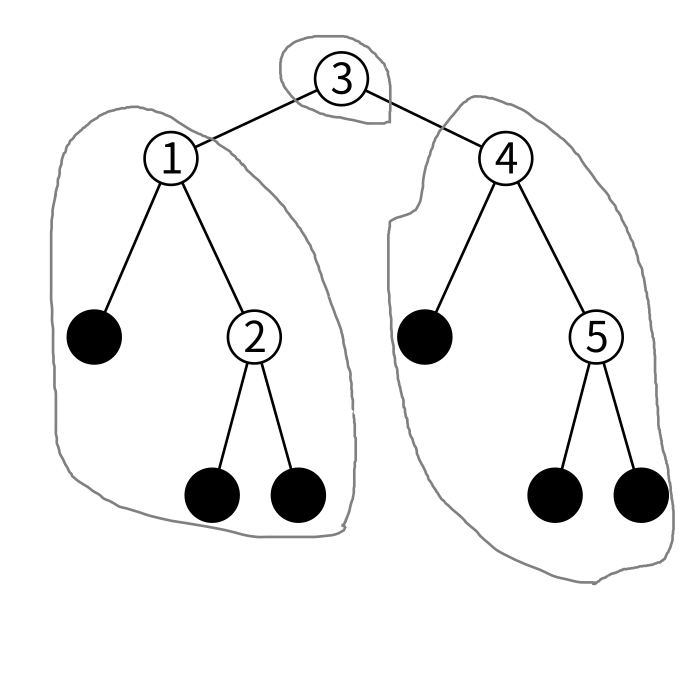
今回は非平衡二分木なので条件はここまでです。 平衡二分木だとここからさらに「左右が大体同じくらいの高さ」という条件が付きます。
二分木への操作
まずは検索と挿入を説明しましょう。
検索
検索は二分探索をそのまま行えます。 例えば先程の1, 2, 3, 4, 5を保持している木に2が含まれるか検索してみましょう。
まず3と2を比較します。2は3より小さいので、あるとしたら左の子にあるはずです。右の子は3より大きい値しか保持していないので絶対ありません。左の子を見てみましょう。
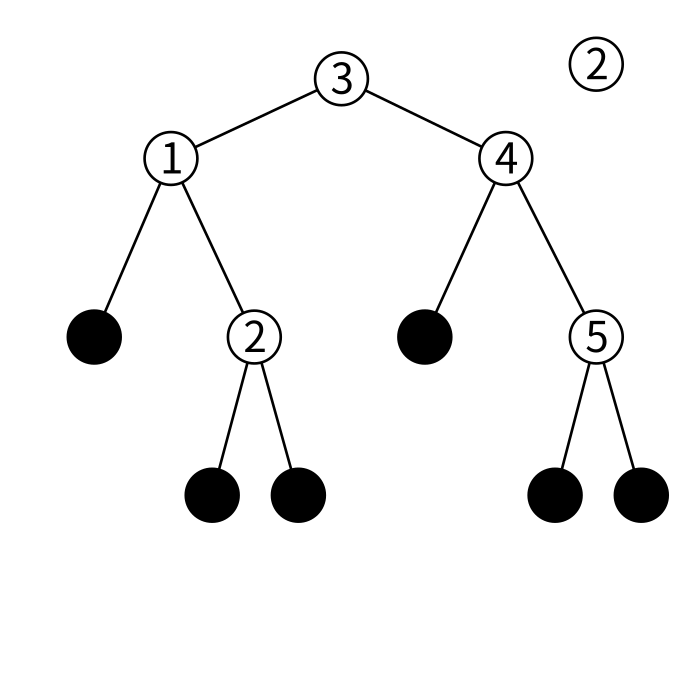
左の子は1を保持しています。2は1より大きいのであるとしたら右の子にあるはずです。右の子をみてましょう。
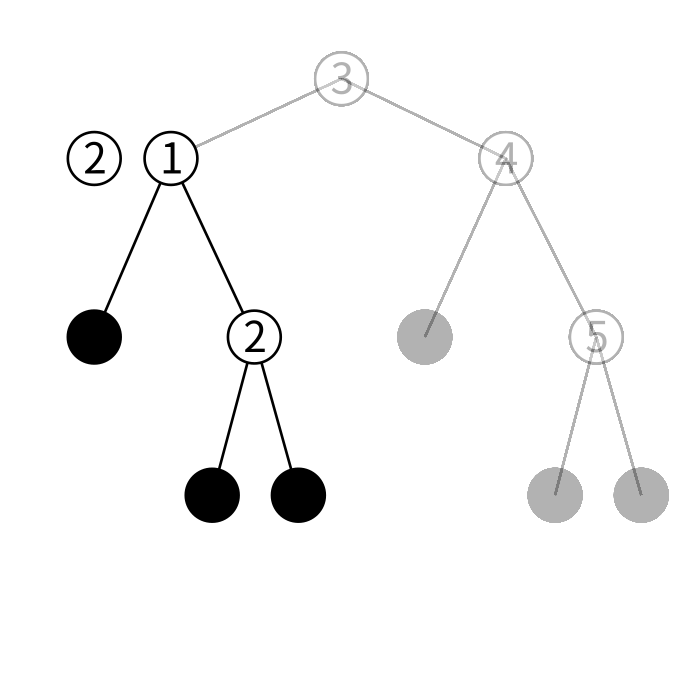
右の子は2を保持しています。検索している値が見つかったのでこの木に2が含まれることが分かります。
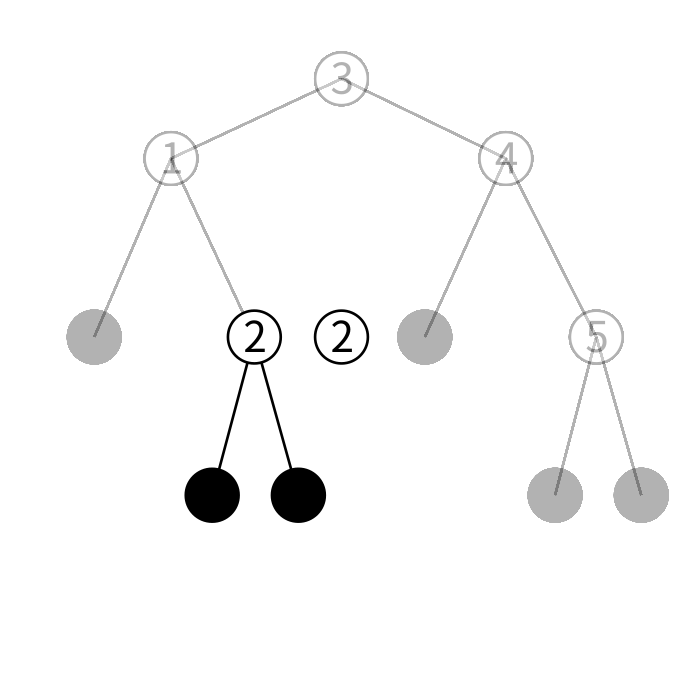
同様の検索をして、葉に行き当たったら検索している値はなかったということが分かります。
挿入
挿入も検索と似たようなことをします。先程の木に6という値を挿入してみましょう。
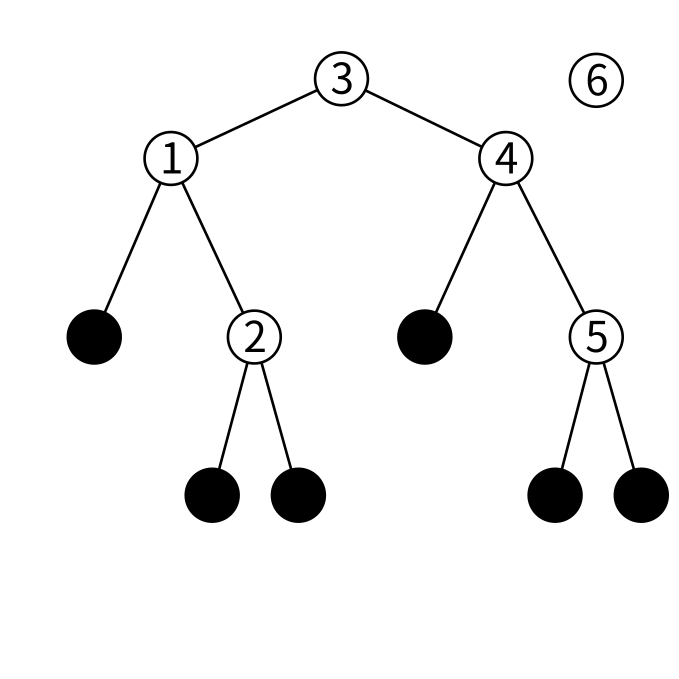
6は3より大きいので右の子を見ます。
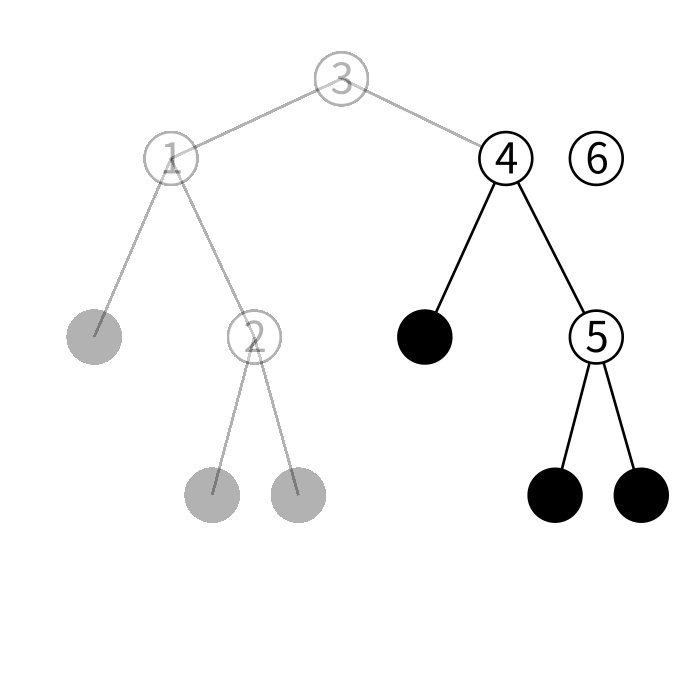
右の子を見ると6は4より大きいのでさらに右の子を見ます。
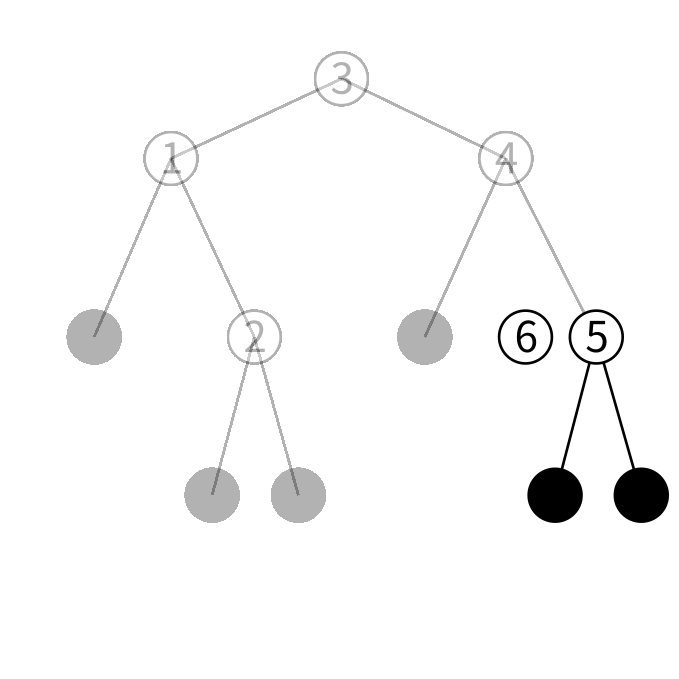
6は5より大きいので更に右の子を見ます。
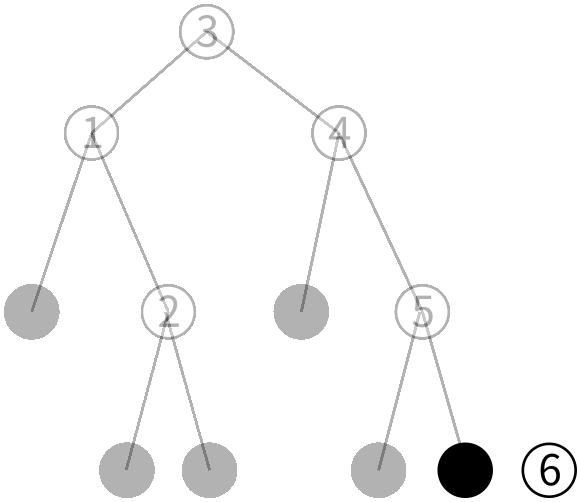
右の子はリーフなのでこの木には6がいないことが分かりました。 そこで6だけを保持する 新しいノードを作ります。
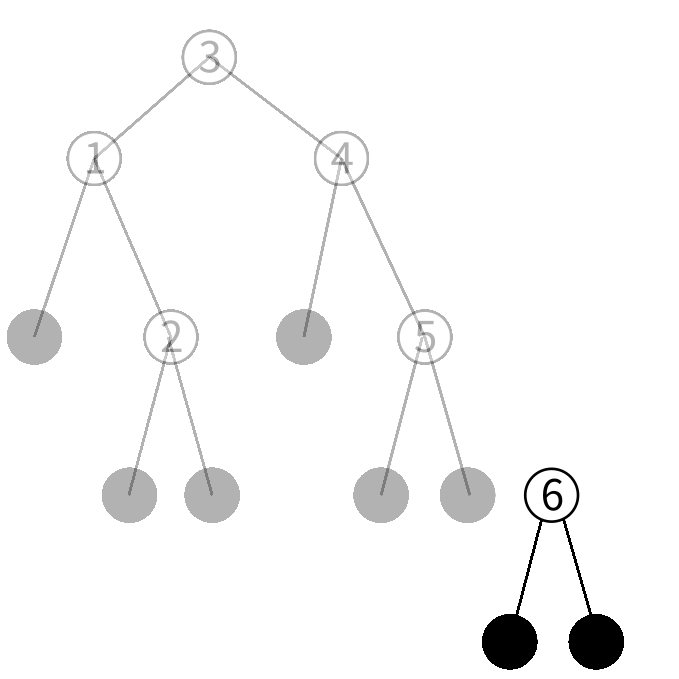
5を保持するノードの右の子を今作ったノードにした 新しいノードを作ります。
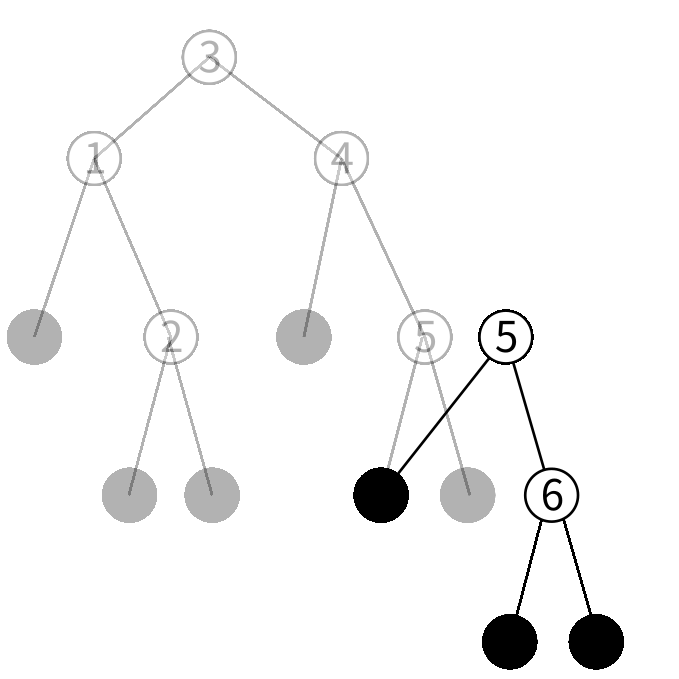
4を保持するノードの右の子を今作ったノードにした 新しいノードを作ります。
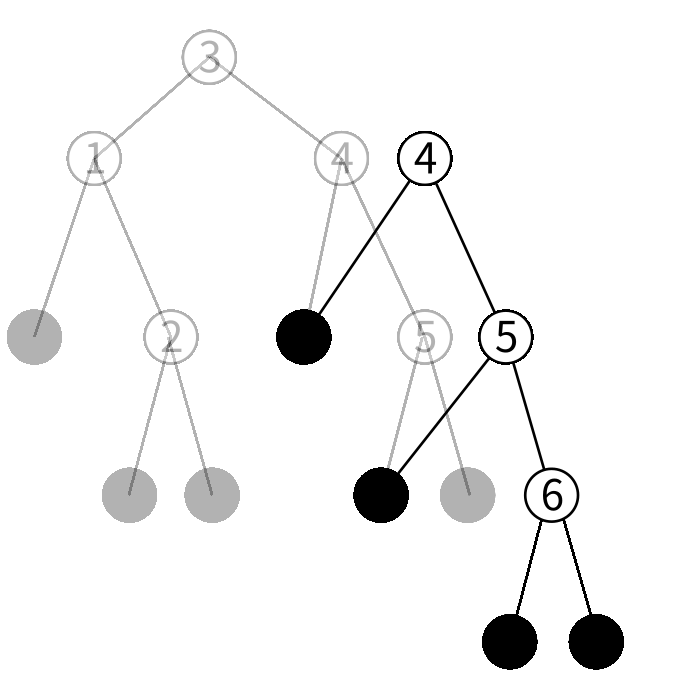
3を保持するノードの右の子を今作ったノードにした 新しいノードを作ります。
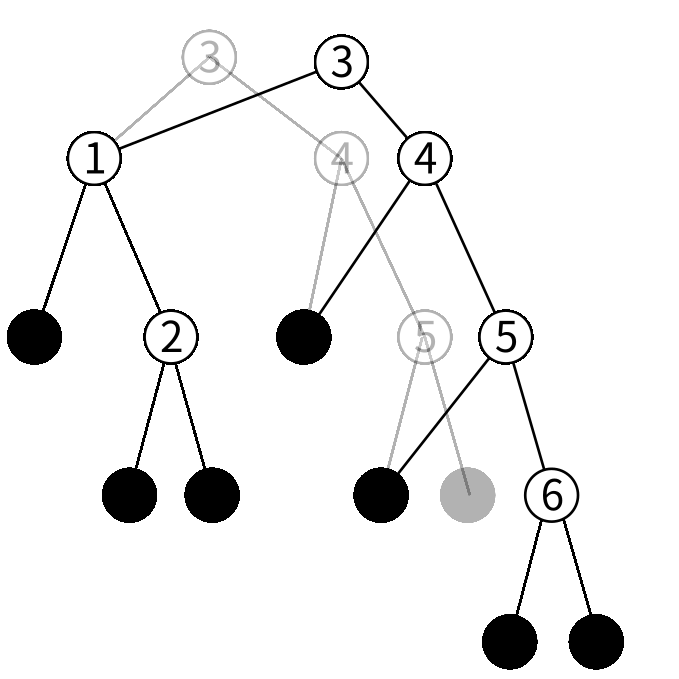
これで更新が完了しました。
更新というよりは挿入する値も保持した新しい木を作る操作ですね。 Idrisは純粋関数型言語なので破壊的変更ができません。 なので更新ではなく新しい値を作ることになります。そういったときに部分構造を共有できる二分木は無駄が少なく、効率的なデータ構造になるのです。 また、更新したあとも古い値が使える、データが順に保持される、などのおまけ付きです。
二分木の実装
さて、座学はこのくらいにして実装していきましょう。
データ型の定義
まずはデータ構造の定義です。二分木とはリーフ、または2つの子と値を持ったノードからなるのでした。 BTree.idrに以下を実装します。
module BTree
data BTree a = Leaf
| Node (BTree a) a (BTree a)
これはデータ型の定義です。BTree a というのは a 型の値を保持するBTreeという意味です。ジェネリクスになってますね。
定義の中身は Leaf または Node です。 Leaf はデータを持ちません。 Node は2つの子(BTree a)と 値(a)を持ちます。
Leaf や Node のことをヴァリアントだとか列挙子だとかコンストラクタだとか呼びます。
コンストラクタの別名のとおり、BTree の値を作るにはこれらのコンストラクタを使います。Leaf は値のように、 Node は関数のように使えます。
数当てゲームのところで Either などを扱ったので馴染んでいますね。
REPLで少し遊んでみましょう。
まずは Leaf はBTreeです。
λΠ> Leaf
(input):Can't infer argument a to Leaf
おっと、いきなり起こられました。BTree は多相(ジェネリクス)なので Leaf だけではパラメータの部分、 BTree a の a の部分の型が決まらないのです。
BTree Integer であることを明示しましょう。それには the 型名 式 が使えます。
λΠ> the (BTree Integer) Leaf
Leaf : BTree Integer
余談ですが the はキーワードではなくただの関数です。
λΠ> :t the
the : (a : Type) -> a -> a
型を関数の引数に渡せてしまうところがIdrisの特徴です。
閑話休題。ノードの方を試してみましょう。ノードを使うといくらでも複雑な構造を作れます。
λΠ> Node Leaf 1 Leaf
Node Leaf 1 Leaf : BTree Integer
λΠ> Node (Node Leaf 1 Leaf) 2 (Node Leaf 3 Leaf)
Node (Node Leaf 1 Leaf) 2 (Node Leaf 3 Leaf) : BTree Integer
必ず最後は Leaf になってることが分かるかと思います。
ところで、以下のような定義も実行できてしまいます。
λΠ> Node (Node Leaf 1 Leaf) 3 (Node Leaf 2 Leaf)
Node (Node Leaf 1 Leaf) 3 (Node Leaf 2 Leaf) : BTree Integer
これは3の右の子に2がきているので今回扱おうとしている二分木としては不適格です。
不適格なデータを作れてしまう問題はデータ型だけではどうしようもないのでプログラマが気をつける必要があります。
挿入
このデータ型に対して挿入を実装してみましょう。まずは型は木 BTree a と値 a を受け取って新しい BTree a を返すのでこうなりそうです。
insert : BTree a -> a -> BTree a
実装の方はリーフかノードかで分岐が発生します。 以下のように書けるでしょう。
insert tree x = case tree of
Leaf => -- ...
Node l v r => -- ...
しかし引数で分岐するときは別の記法があります。以下のように書けるのです。
insert Leaf x = -- ...
insert (Node l v r) x = -- ...
こちらの方がより宣言的で読みやすいスタイルだとされています。 数学の記法に似ていますね。
\[ \begin{align} 0! & = & 0 \\\ n! & = & n * (n-1)! \end{align} \]
余談: エディタサポート
今の実装は実は自動化できます。 型を書いたところまで巻き戻ってみましょう。
insert : BTree a -> a -> BTree a
この状態でinsertにカーソルを合わせてaddclauseと呼ばれるコマンド(EmacsならC-c C-s, Vimなら \d)を打つとこうなります。
insert : BTree a -> a -> BTree a
insert x y = ?insert_rhs
変数名が適当ですが定義のモックが自動生成されました。? マークで始まるのは穴(Hole)と呼ばれ、「あとで実装する」のマークです。詳しくはドキュメントを読んで下さい。
名前はおいておいて、エディタサポートの話を続けます。ここでの x で分岐したいのでした。
x にカーソルを合わせてcasesplitと呼ばれるコマンド(Emacsなら C-c C-c, Vimなら \c)を打つとこうなります。
insert : BTree a -> a -> BTree a
insert Leaf y = ?insert_rhs_1
insert (Node x z w) y = ?insert_rhs_2
ここまで自動生成できました。
自動生成はできたので満足ですが、生成された変数の名前が x, y と適当なのが気になりますよね。
自動生成される名前を制御するにはこのチュートリアルを大きく超える内容が必要です。
型には %name ディレクティブを、ヴァリアントにはGADTを使ってそれぞれこう定義したら目的を達成できます。
data BTree : (a : Type) -> Type where
Leaf : BTree a
Node : (l: BTree a) -> (v: a) -> (r: BTree a) -> BTree a
%name BTree tree, tree1, tree2
これで生成したコードは以下です。
insert: BTree a -> a -> BTree a
insert Leaf x = ?insert_rhs_1
insert (Node l v r) x = ?insert_rhs_2
記法やコンパイラ補助の違いだけで、元の記法もこちらの記法も同じデータ型を定義しているので盲目的に定義を置き換えてしまうのも手です。
さて、これから実装していきましょう。
まずはLeafの方です。Leaf なら新しい値を持ったノードで置き換えるのでした。
Leaf はこう実装できるでしょう。
insert: Ord a => BTree a -> a -> BTree a
insert Leaf x = Node Leaf x Leaf
insert (Node l v r) x = ...
Node の方は大きいか小さいかで分岐が発生しますね。
先程は触れませんでしたが既に同じ値がある場合も新しくノードを作って返すことにします。
比較の3種類の分岐は compare が便利でした。早速こう書いてみましょう。
insert: Ord a => BTree a -> a -> BTree a
insert Leaf x = Node Leaf x Leaf
insert (Node l v r) x = case compare x v of
LT => ?LT
EQ => ?EQ
GT => ?GT
しかしこれはエラーになります。
- + Errors (1)
`-- BTree.idr line 18 col 24:
When checking right hand side of insert with expected type
BTree a
Can't find implementation for Ord a
少し分かりづらいですが、「a に Ord の実装がない」と言っています。
ジェネリクス a はなんでも受け取れます。どんな型がくるか分からないので値の比較が出来る保証もありません。
比較可能かも分からない a を比較しているのでエラーが出ている、というのが直接的原因です。
ではどうやったら修正できるか、はインターフェースの知識が必要なのでインターフェースについて説明します。
インターフェース
インターフェースはデータ型間で共通の操作を定義する機能です。 インターフェースは以下の構文で定義でます。
-- わかりやすさのため微妙に嘘をついてます
interface インターフェース名 対象の型 where
関数1 : 型
関数2 : 型
...
デフォルト実装(あれば)
...
where 以降はオフサイドルールですね。インターフェースの関数はメソッドと呼びます。
例えば色々な型の値を文字列として表示可能にするインターフェース Show はこう定義されています。
interface Show a where
show : a -> String
あるいは同値比較のインターフェース Eq はこう定義されています。
-- 括弧がついている関数名は中置記法で使われる(あまり気にしなくていいです)
interface Eq a where
(==) : a -> a -> Bool
(/=) : a -> a -> Bool
x /= y = not (x == y)
x == y = not (x /= y)
インターフェースは以下の構文で個々のデータ型に実装できます。
インターフェース名 対象の型 where
関数1 = 実装
関数2 = 実装
適当なデータ型を定義して Show と Eq を実装してみましょう。
data Camellia = Japonica | Sasanqua
Eq Camellia where
(==) Japonica Japonica = True
(==) Sasanqua Sasanqua = True
(==) _ _ = False
Show Camellia where
show Japonica = "Japonica"
show Sasanqua = "Sasanqua"
そして「Show を実装した型を受け取る」はこう書けます。型定義の前に Show a => を置くのです。
print : Show a => a -> IO ()
print = putStr $ show
この型定義を読み下すなら「Show を実装した型 a に対して、 a を受け取って IO () を返す関数」となるでしょう。
ということで先程の答えが出ました。 Ord が目的のインターフェースなので Ord a => を追加すればよさそうです。
insert 関数の型定義に戻って Ord a => を追加しましょう。
insert: Ord a => BTree a -> a -> BTree a
これで比較ができるようになったのであとは実装するだけです。 等しい場合は簡単ですね。そのまま作り直すだけです。
insert (Node l v r) x = case compare x v of
LT => ?LT
EQ => Node l v r
GT => ?GT
小さい場合は左の子(l)を、それに x 挿入したもので置き換えるのでした。大きい場合はその対称ですね。
つまり実装はこうなります。
insert (Node l v r) x = case compare x v of
LT => Node (insert l x) v r
EQ => Node l v r
GT => Node l v (insert r x)
insert が実装できました。
検索の方は簡単なので適当に実装して下さい。
member : Ord a => BTree a -> a -> Bool
member Leaf x = False
member (Node l v r) x = case compare x v of
LT => member l x
EQ => True
GT => member r x
さて、ひとまずデータを入れて検索するところまでいけました。
地味に、空の木を表す empty も作っておきましょう。
empty : BTree a
empty = Leaf
関数ではなく値です。Idrisは純粋関数型言語なので更新される心配がなく、empty を値として定義して使いまわしても何も問題がありません。
少しREPLで試してみて下さい。 :let で束縛を作れるのでそれを使うと良いでしょう。
λΠ> :let tree = insert empty 1
defined
λΠ> tree
Node Leaf 1 Leaf : BTree Integer
λΠ> member tree 1
True : Bool
λΠ> member tree 2
False : Bool
λΠ> :let tree = insert tree 3
defined
λΠ> tree
Node Leaf 1 (Node Leaf 3 Leaf) : BTree Integer
λΠ> member tree 1
True : Bool
λΠ> member tree 2
False : Bool
λΠ> member tree 3
True : Bool
テスト
機能するものができたので自動テストをしてみましょう。 テストは2, 3個の例を試して正しく動くか試す、ソフトウェアの品質検査法です。 数学の試験で2, 3個の例を試して正しい、などと書いたら正解になりませんが、明らかな誤りを見つけるにはこれでも効果はあります。
新しくテストディレクトリを作り、そこに BTree.idr を作りましょう。
├── btree.ipkg
└── src
├── BTree.idr
└── Tests
└── BTree.idr
そして btree.ipkg を編集します。
package btree
sourcedir = src
modules = BTree
, Tests.BTree
tests = Tests.BTree.test
pkgs = contrib
テストモジュールをモジュールリストに加える、テストのエントリーポイントを指定する、依存パッケージにcontribを追加する、をやっています。
contribはIdrisコンパイラと一緒に配布されているパッケージですが、デフォルトではリンクされません。 idrisは標準ライブラリへの機能追加に保守的な方針を取っています。まずはcontribライブラリに入れ、誰が見ても必要だと判断できたらデフォルトでリンクされるpreludeやbaseに入ります。 今回はcotribにあるテストライブラリを使います。
さて、テストを書いていくのですが、その前に先程定義したデータ型を公開しないといけません。
モジュールと可視性
前回のチュートリアルでモジュールについては学習したと思います。まだの人はドキュメントを読んでおいて下さい。
Idrisには3つの可視性の修飾子があります。
private- モジュール内でのみ見えるexport- モジュール外から型が見える。他言語でいうパブリックに近いpublic export- モジュール外から型と実装が見える。つまり実装の詳細まで公開APIになる
public export はかなり危険ですが、データ型だとコンストラクタまで公開したいケースは多々あるので便利でしょう。
今回は二分木に「ノードの左の子に保持されている全ての値よりもノードの保持している値の方が大きい。ノードの右の子に保持されている全ての値よりも値の方が小さい。」という条件があります。
ユーザにコンストラクタまで公開すると条件を満たさない木を作られかねないので public export ではなく export にします。
今ある4つの定義に export をつけましょう。
export
data BTree ..
export
empty: BTree a
...
export
insert: Ord a => BTree a -> a -> BTree a
export
member : Ord a => BTree a -> a -> Bool
さて、これでテストが書けます。 Test.Unit.Assertionsを使ってテストを書いてみましょう。 Tests/BTree.idrにこう書きます。
module Tests.BTree
import BTree
import Test.Unit.Assertions
testInsertMember : IO ()
testInsertMember =
let tree = insert empty 1 in
let tree = insert tree 5 in
let tree = insert tree 3 in
do
assertTrue $ member tree 1
assertTrue $ member tree 5
assertTrue $ member tree 3
pure ()
assertTrue を使って insert して member したら存在するということをテストしています。
let 変数 = 式1 in 式2 はローカル変数を導入する構文です。
ネストするときはこのようにインデントを揃えると見慣れたコードに近くなります。
最後にテストのエントリーポイントを書きます。
export
test : IO ()
test = do
testInsertMember
test はipkgで指定した名前です。
このテストを走らせます。コマンドラインで idris --testpkg btree.ipkg を打つとテストが走ります。
$ idris --testpkg btree.ipkg
Entering directory `./src'
Type checking /tmp/idris74355-0.idr
Test: Assert True
Test: Assert True
Test: Assert True
Leaving directory `./src'
上手くいっているようです。
テストをもう少し追加しましょう。 insert してない値を member したら False になるテストです。
テストを書き、
testNotInsertMember : IO ()
testNotInsertMember =
let tree = insert empty 1 in
let tree = insert tree 5 in
let tree = insert tree 3 in
do
assertFalse $ member tree 2
assertFalse $ member tree 4
pure ()
エントリーポイントに追加し、
export
test : IO ()
test = do
testInsertMember
testNotInsertMember
実行します。
$ idris --testpkg btree.ipkg
Entering directory `./src'
Type checking ./Tests/BTree.idr
Type checking /tmp/idris74537-0.idr
Test: Assert True
Test: Assert True
Test: Assert True
Test: Assert False
Test: Assert False
Leaving directory `./src'
問題ないですね。
削除
削除はまず検索と同じ要領で要素を見つけます。 例えば3を削除するとしましょう。3は簡単に見つかります。
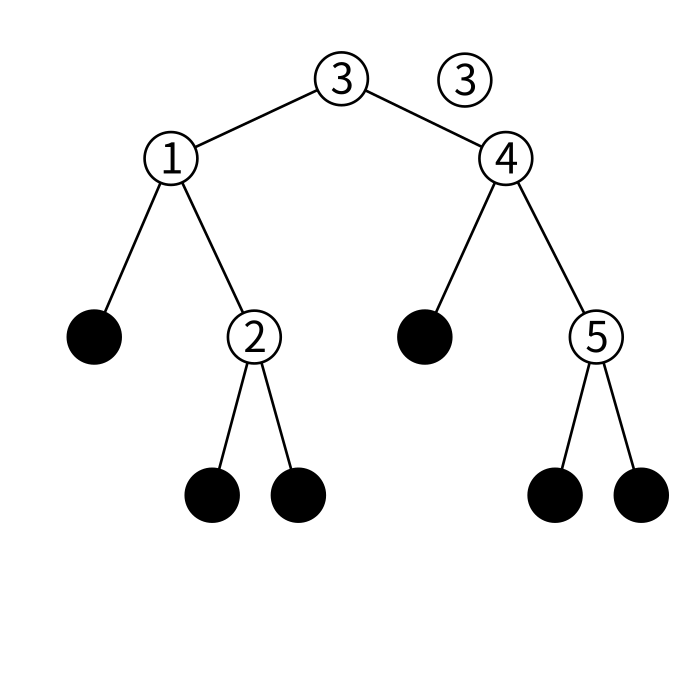
ここから3以外(要は左右の子)で新しく木を作ります。
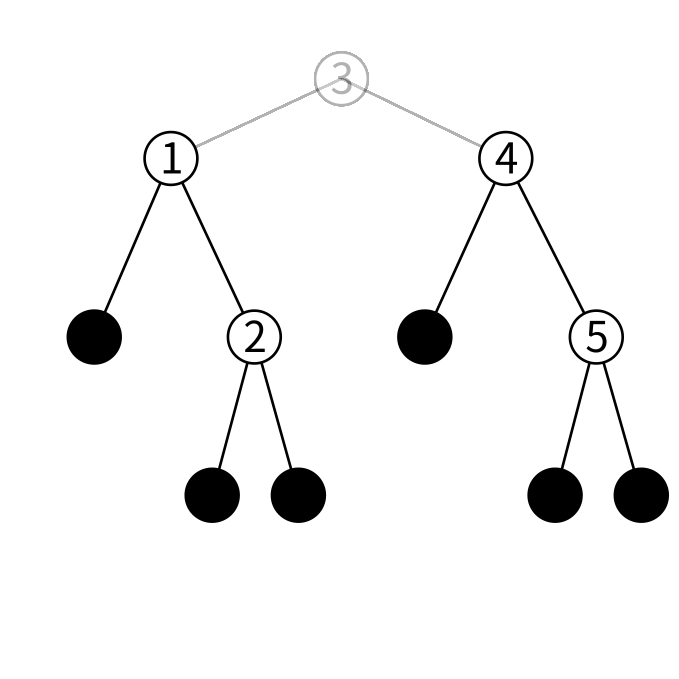
ノードを1つ追加すれば出来るのですが、ノードに保持する値が必要です。 左の子の最大値を持ってきてあげると上手くいきます。
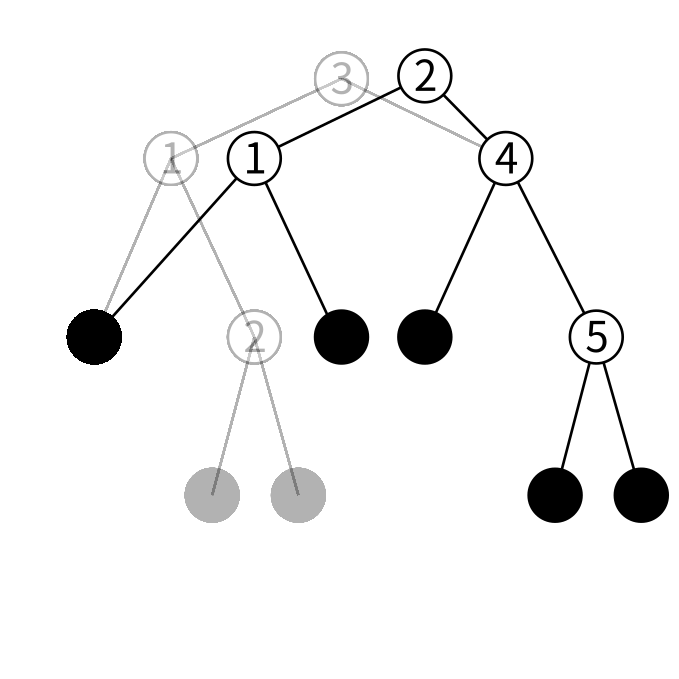
これにはサブルーチン、popMaxを使います。 「ノードの値が木の最大値である⇒右の子がリーフ」なので簡単に発見、削除できます。
ずっと右の子を辿っていって右の子がリーフであるノードを見つけたらそのノードの値が最大値です。
空の木の場合は最大値がないので注意しましょう。
export
popMax : BTree a -> (BTree a, Maybe a)
popMax Leaf = (Leaf, Nothing)
popMax (Node l v Leaf) = (l, Just v)
popMax (Node l v r) = let (r', max) = popMax r in
(Node l v r', max)
ここで (BTree a, Maybe a) と書いてあるのはタプル(組)の型です。 簡易版構造体のようなもので、複数の値をひとまとめにできます。そして (Leaf, Nothing) のように書いてあるのがタプルの値です。
今更ですが、ちょくちょく出てきていた () は空のタプルのことでした。
この popMax を使うと delete はこう書けます。 member とほとんど似た見た目ですが EQ の腕で popMax を呼ぶようになっています。
export
delete : Ord a => BTree a -> a -> BTree a
delete Leaf x = Leaf
delete (Node l v r) x = case compare x v of
LT => Node (delete l x) v r
GT => Node l v (delete r x)
EQ => case popMax l of
(l', Just max) => Node l' max r
(l', Nothing) => r -- l' = Leaf
これもテストしておきましょう。
testDelete : IO ()
testDelete =
let tree = insert (the (BTree Integer) empty) 1 in
let tree = insert tree 5 in
let tree = insert tree 3 in
do
assertTrue $ member tree 1
let tree = delete tree 1
assertFalse $ member tree 1
pure ()
testPopMax : IO ()
testPopMax =
let tree = insert empty 1 in
let tree = insert tree 5 in
let tree = insert tree 3 in
do
let (tree, max) = popMax tree
assertEquals max (Just 5)
let (tree, max) = popMax tree
assertEquals max (Just 3)
let (tree, max) = popMax tree
assertEquals max (Just 1)
let (tree, max) = popMax tree
assertEquals max Nothing
pure ()
export
test : IO ()
test = do
-- ...
testPopMax
testDelete
練習問題として popMin も実装してみて下さい。
雑多な操作
二分木には色々な操作ができます。
最大値、最小値
例えば最大値、最小値は簡単に求まります。popMax, popMin の亜種ですね。
export
max: BTree a -> Maybe a
max Leaf = Nothing
max (Node _ v Leaf) = Just v
max (Node _ _ r) = max r
export
min: BTree a -> Maybe a
min Leaf = Nothing
min (Node Leaf v _) = Just v
min (Node l _ _) = min l
分割
木を分割してみましょう。値 x を取り、「x より小さい値を含んだ木、x が含まれれば x 、 x より大きい値を含んだ木」の3つ組を返します。
export
split: Ord a => BTree a -> a -> (BTree a, Maybe a, BTree a)
split Leaf x = (Leaf, Nothing, Leaf)
split (Node l v r) x = case compare x v of
LT => let (ll, lv, lr) = split l x in (ll, lv, Node lr v r)
EQ => (l, Just v, r)
GT => let (rl, rv, rr) = split r x in (Node l v rl, rv, rr)
Foldabe
Foldable というインターフェースがプレリュードで定義されています。
||| The `Foldable` interface describes how you can iterate over the
||| elements in a parameterised type and combine the elements
||| together, using a provided function, into a single result.
|||
||| @t The type of the 'Foldable' parameterised type.
interface Foldable (t : Type -> Type) where
||| Successively combine the elements in a parameterised type using
||| the provided function, starting with the element that is in the
||| final position i.e. the right-most position.
|||
||| @func The function used to 'fold' an element into the accumulated result.
||| @input The parameterised type.
||| @init The starting value the results are being combined into.
foldr : (func : elem -> acc -> acc) -> (init : acc) -> (input : t elem) -> acc
||| The same as `foldr` but begins the folding from the element at
||| the initial position in the data structure i.e. the left-most
||| position.
|||
||| @func The function used to 'fold' an element into the accumulated result.
||| @input The parameterised type.
||| @init The starting value the results are being combined into.
foldl : (func : acc -> elem -> acc) -> (init : acc) -> (input : t elem) -> acc
foldl f z t = foldr (flip (.) . flip f) id t z
foldl 、 foldr は概ねループをする関数です。foldl が左から、 foldre が右からの巡回です。
foldl は数当てゲームで使いましたね。
Foldable は他言語でいう Iterable みたいなものです。ただし関数型風味です。
変更可能な状態を持てないので外部イテレータではなく内部イテレータで定義されています。そしてループの途中の計算状態 acc を持ち回ります。
これを二分木に実装しましょう。foldl は 「まず左、値、そして右」の順(通りがけ順)に走査していけばよさそうです。
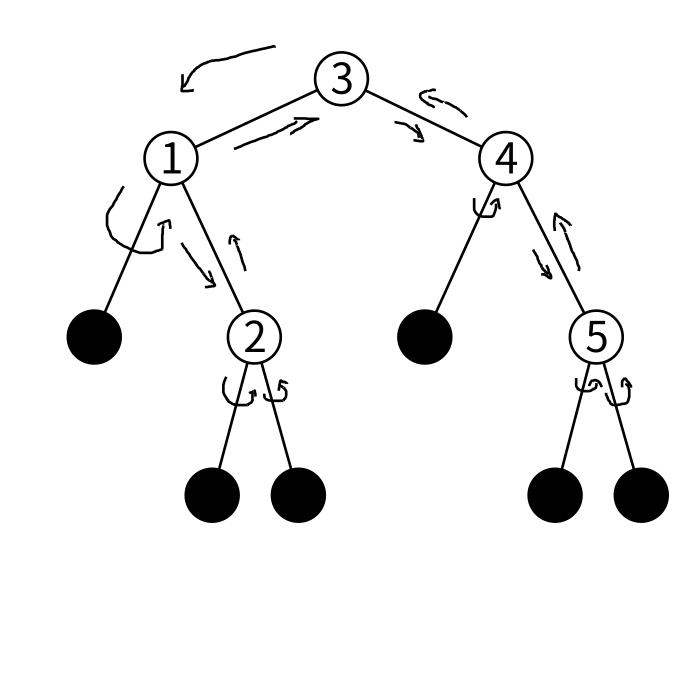
foldr はその対称ですね。
素直にこう実装できます。
Foldable BTree where
foldr f init Leaf = init
foldr f init (Node l v r) =
let r = foldr f init r in
let v = f v r in
foldr f v l
foldl f init Leaf = init
foldl f init (Node l v r) =
let l = foldl f init l in
let v = f l v in
foldl f v r
これを用いてリストとの相互変換を実装してみましょう。 煩雑だった値の構築が少し楽になります。
export
toList: BTree a -> List a
toList tree = foldr (::) [] tree
export
toTree: Ord a => List a -> BTree a
toTree xs = foldl insert empty xs
ここで、 (::) はリストのコンストラクタです。
λΠ> the (List Integer) $ 1 :: 2 :: 3 :: []
[1, 2, 3] : List Integer
fold
先程の foldr, foldl とは別に fold という関数が定義できます。
BTree は以下のように定義されているのでした。
data BTree a = Leaf
| Node (BTree a) a (BTree a)
BTree は定数 Leaf と3引数関数 Node で構成されているとも読めます。fold は この構成子を別の定数と3引数関数で置き換えてあげる操作です。
リストは foldr がそのまま fold に対応するのですが BTree はそうではないので自分で定義します。
export
fold: BTree a -> b -> (b -> a -> b -> b) -> b
fold Leaf x f = x
fold (Node l v r) x f = f (fold l x f) v (fold r x f)
Leaf -> x 、 Node -> f を再帰的にやっているのが見て取れると思います。
fold を使っていくつか関数を定義してみましょう。
木のサイズ(保持している要素数)はこう定義できます。
export
size : BTree a -> Integer
size tree = fold tree 0 (\l, _, r => l + 1 + r)
木の高さは以下のように定義できます
- リーフの高さは0である
- ノードの高さは左右の子の高さのうち大きい方+1である
これも同様に fold で求められます。
export
height : BTree a -> Integer
height t = fold t 0 (\lh,_,rh => (max lh rh) + 1)
これは一番深い方を求めています。浅い方を求めるのも考えられるのでそれも実装してみましょう。
export
maxHeight : BTree a -> Integer
maxHeight t = fold t 0 (\lh,_,rh => (max lh rh) + 1)
export
minHeight : BTree a -> Integer
minHeight t = fold t 0 (\lh,_,rh => (min lh rh) + 1)
export
height : BTree a -> Integer
height = maxHeight
余談: fold の一般化
fold はBTreeやリストに限らず色々なデータ型にも定義できますが、それをインターフェースで一般化するのはかなり難易度が上がります。
列挙子に応じて引数の数や型が変わるので共通のインターフェースが定められないのです。
やるとしたらデータ型の定義ごと管理下に置くような仕組みが必要になるでしょう。
そういうのは"recursion scheme"という名前で色々整備されているようです。fold はcatamorphismと呼ばれます。
resursion schemeは日本語でもいくつか解説があるようですが以下のブログを紹介しておきます。
#003 代数的データ型 - λx.x K S K @ はてな
集合操作
二分木は集合のように扱えるので合併、交叉、差分などの操作も欲しくなりますよね。
foldl を使うと簡単に実装できます。
union : Ord a => BTree a -> BTree a -> BTree a
union tree1 tree2 = foldl insert tree1 tree2
-- `if` 式は `if 条件 then 式 else 式` で書く
intersection : Ord a => BTree a -> BTree a -> BTree a
intersection tree1 tree2 = foldl (\acc,elm => if member tree1 elm
then insert acc elm
else acc)
empty tree2
difference : Ord a => BTree a -> BTree a -> BTree a
difference tree1 tree2 = foldl delete tree1 tree2
union は少し良くない点があるのですが気にしないことにしましょう。
さて、これらの雑多な操作のテストも書いておきましょう。
testToTreeMember : IO ()
testToTreeMember =
let tree = toTree [1, 5, 3] in
do
assertTrue $ member tree 1
assertTrue $ member tree 5
assertTrue $ member tree 3
pure ()
testToTreeToList : IO ()
testToTreeToList =
let tree = toTree [1, 5, 3] in
let list = toList tree in
do
assertEquals list [1, 3, 5]
pure ()
testMax : IO ()
testMax =
let tree = toTree [1, 4, 3, 5, 2] in
do
assertEquals (max tree) (Just 5)
pure ()
testMin : IO ()
testMin =
let tree = toTree [1, 4, 3, 5, 2] in
do
assertEquals (min tree) (Just 1)
pure ()
testSplit1 : IO ()
testSplit1 =
let tree = toTree [1, 5, 3, 2, 4] in
let (l, v ,r) = split tree 3 in
do
assertEquals (toList l) [1, 2]
assertEquals v (Just 3)
assertEquals (toList r) [4, 5]
pure ()
testSplit2 : IO ()
testSplit2 =
let tree = toTree [1, 5, 2, 4] in
let (l, v ,r) = split tree 3 in
do
assertEquals (toList l) [1, 2]
assertEquals v Nothing
assertEquals (toList r) [4, 5]
pure ()
testSplit3 : IO ()
testSplit3 =
let tree = toTree [1, 5, 2, 4] in
let (l, v ,r) = split tree 6 in
do
assertEquals (toList l) [1, 2, 4, 5]
assertEquals v Nothing
assertEquals (toList r) []
pure ()
testSplit4 : IO ()
testSplit4 =
let tree = toTree [1, 5, 2, 4] in
let (l, v ,r) = split tree 0 in
do
assertEquals (toList l) []
assertEquals v Nothing
assertEquals (toList r) [1, 2, 4, 5]
pure ()
testSplit : IO ()
testSplit = do
testSplit1
testSplit2
testSplit3
testSplit4
testUnion : IO ()
testUnion =
let tree1 = toTree [1, 3, 5] in
let tree2 = toTree [2, 3, 4] in
let tree = union tree1 tree2 in
do
assertEquals (toList tree) [1, 2, 3, 4, 5]
pure ()
export
test : IO ()
test = do
-- ...
testToTreeMember
testToTreeToList
testMax
testMin
testSplit
testUnion
パッケージを整える
btree.ipkgには最低限の内容しか書いてませんでした。色々埋めましょう。
brief = "A non-balanced Binary Tree library"
version = "0.1.0"
readme = "README.md"
license = "MIT"
author = "κeen"
maintainer = "κeen"
sourceloc = "https://gitlab.com/blackenedgold/idris-btree"
bugtracker = "https://gitlab.com/blackenedgold/idris-btree/issues"
ドキュメントを生成してみましょう。
$ idris --mkdoc btree.ipkg
btree_doc/index.html を開くとドキュメントを確認できます。
あとは .gitignore を書いて適当にコミットしましょう。
*.ibc
btree_doc
コードホスティングサービスにGitLabを使うならGitLab CIで以下のようにテスト/ドキュメント生成ができます。
# インターネットに転がっていたイメージ
# 得体のしれないイメージを使いたくない人は自分でイメージを作ると良い
image: mmhelloworld/idris:1.3.1
test:
script:
- idris --testpkg btree.ipkg
pages:
script:
- idris --mkdoc btree.ipkg
# docker内で生成するとパーミッションの問題が発生するらしく、ディレクトリを一旦作り直すと解決する
- mkdir public
- cp -R btree_doc/* public
artifacts:
paths:
- public
only:
- master
生成されたドキュメントはこちら。 GitHubでも外部サービスやGitHub Actionsで同様にはできると思います。ドキュメントの方はGitLab Pagesとは違って一苦労必要そうですが。
まとめ
このチュートリアルでは二分木のライブラリを作りつつIdrisでのデータ型の定義、インターフェース、テスト、パッケージなどについて学びました。